PythonRobotics机器人算法库-火箭动力着陆

说明：

• 介绍如何模拟火箭动力着陆

• 参考代码

步骤：

• 模拟

from IPython.display import Image
Image(filename="figure.png",width=600)
from IPython.display import display, HTML

display(HTML(data="""
<style>
    div#notebook-container    { width: 95%; }
    div#menubar-container     { width: 65%; }
    div#maintoolbar-container { width: 99%; }
</style>
"""))

• 方程生成

import sympy as sp
import numpy as np
from IPython.display import display
sp.init_printing(use_latex='mathjax')

# parameters
# Angular moment of inertia
J_B = 1e-2 * np.diag([1., 1., 1.])

# Gravity
g_I = np.array((-1, 0., 0.))

# Fuel consumption
alpha_m = 0.01

# Vector from thrust point to CoM
r_T_B = np.array([-1e-2, 0., 0.])


def dir_cosine(q):
        return np.matrix([
            [1 - 2 * (q[2] ** 2 + q[3] ** 2), 2 * (q[1] * q[2] +
                                                   q[0] * q[3]), 2 * (q[1] * q[3] - q[0] * q[2])],
            [2 * (q[1] * q[2] - q[0] * q[3]), 1 - 2 *
             (q[1] ** 2 + q[3] ** 2), 2 * (q[2] * q[3] + q[0] * q[1])],
            [2 * (q[1] * q[3] + q[0] * q[2]), 2 * (q[2] * q[3] -
                                                   q[0] * q[1]), 1 - 2 * (q[1] ** 2 + q[2] ** 2)]
        ])

def omega(w):
        return np.matrix([
            [0, -w[0], -w[1], -w[2]],
            [w[0], 0, w[2], -w[1]],
            [w[1], -w[2], 0, w[0]],
            [w[2], w[1], -w[0], 0],
        ])

def skew(v):
    return np.matrix([
            [0, -v[2], v[1]],
            [v[2], 0, -v[0]],
            [-v[1], v[0], 0]
        ])

f = sp.zeros(14, 1)

x = sp.Matrix(sp.symbols(
    'm rx ry rz vx vy vz q0 q1 q2 q3 wx wy wz', real=True))
u = sp.Matrix(sp.symbols('ux uy uz', real=True))

g_I = sp.Matrix(g_I)
r_T_B = sp.Matrix(r_T_B)
J_B = sp.Matrix(J_B)

C_B_I = dir_cosine(x[7:11, 0])
C_I_B = C_B_I.transpose()

f[0, 0] = - alpha_m * u.norm()
f[1:4, 0] = x[4:7, 0]
f[4:7, 0] = 1 / x[0, 0] * C_I_B * u + g_I
f[7:11, 0] = 1 / 2 * omega(x[11:14, 0]) * x[7: 11, 0]
f[11:14, 0] = J_B ** -1 * \
    (skew(r_T_B) * u - skew(x[11:14, 0]) * J_B * x[11:14, 0])

display(sp.simplify(f)) # f

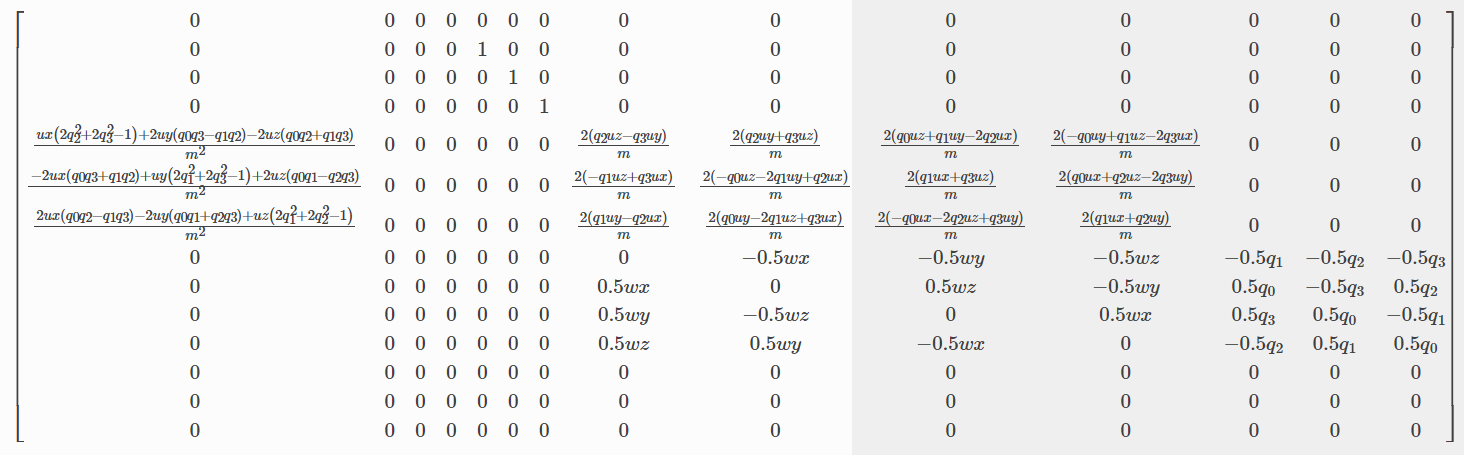
sp.simplify(f.jacobian(u)) # B

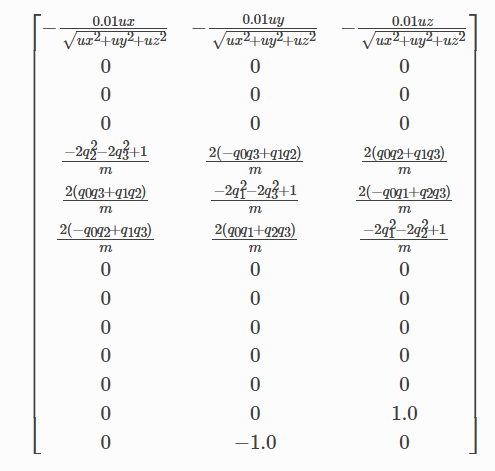
• 进入目录PythonRobotics/AerialNavigation/rocket_powered_landing

• 执行文件

python3 rocket_powered_landing.py

• 结果如下

start!!
------------------ Iteration 01 ------------------
/home/ubuntu/.local/lib/python3.8/site-packages/cvxpy/reductions/solvers/solving_chain.py:178: UserWarning: You are solving a parameterized problem that is not DPP. Because the problem is not DPP, subsequent solves will not be faster than the first one. For more information, see the documentation on Discplined Parametrized Programming, at
    https://www.cvxpy.org/tutorial/advanced/index.html#disciplined-parametrized-programming
  warnings.warn(dpp_error_msg)
delta_norm 44.32276498916253
sigma_norm 9.900000000029438
nu_norm 8.909551753081745e-13
Time for iteration 0.9334554672241211 s
------------------ Iteration 02 ------------------
delta_norm 41365.64683518537
sigma_norm 4.156372350311136
nu_norm 0.47472761962387533
Time for iteration 0.5867664813995361 s
------------------ Iteration 03 ------------------
delta_norm 397.6968271054311
sigma_norm 0.47069903553265746
nu_norm 0.054169365871438634
Time for iteration 0.8205149173736572 s
------------------ Iteration 04 ------------------
delta_norm 139.18165772077353
sigma_norm 0.34408489556612526
nu_norm 5.571014077886119e-12
Time for iteration 0.7841591835021973 s
------------------ Iteration 05 ------------------
/home/ubuntu/.local/lib/python3.8/site-packages/cvxpy/problems/problem.py:1337: UserWarning: Solution may be inaccurate. Try another solver, adjusting the solver settings, or solve with verbose=True for more information.
  warnings.warn(
delta_norm 68.95322460878978
sigma_norm 0.14875083390539423
nu_norm 6.2886597158956085e-12
Time for iteration 0.7790186405181885 s
------------------ Iteration 06 ------------------
delta_norm 20.02983065883662
sigma_norm 0.05750385965702848
nu_norm 1.1770168658673602e-12
Time for iteration 0.7734806537628174 s
------------------ Iteration 07 ------------------
delta_norm 1.2595070208823527
sigma_norm 0.006498594392844756
nu_norm 3.3095370863293516e-12
Time for iteration 0.7507827281951904 s
------------------ Iteration 08 ------------------
delta_norm 0.32027584161219647
sigma_norm 0.01251507046859947
nu_norm 1.3567281169882777e-12
Time for iteration 0.7300641536712646 s
------------------ Iteration 09 ------------------
delta_norm 0.1177038721279697
sigma_norm 0.006784446741462801
nu_norm 1.2847738121837189e-12
Time for iteration 0.7648491859436035 s
------------------ Iteration 10 ------------------
delta_norm 0.047677371973176556
sigma_norm 0.00406408958339929
nu_norm 3.4669671365085466e-12
Time for iteration 0.7454721927642822 s
------------------ Iteration 11 ------------------
delta_norm 0.019915287670014138
sigma_norm 0.0025803064624417577
nu_norm 5.982337042606832e-12
Time for iteration 0.7359716892242432 s
------------------ Iteration 12 ------------------
delta_norm 0.008236431448584571
sigma_norm 0.0015905080696839817
nu_norm 2.4783869061593275e-11
Time for iteration 0.756528377532959 s
------------------ Iteration 13 ------------------
delta_norm 0.003622313239233523
sigma_norm 0.001044227060242893
nu_norm 1.3801401455849377e-11
Time for iteration 0.7574238777160645 s
------------------ Iteration 14 ------------------
delta_norm 0.0015994824668878846
sigma_norm 0.0006917450248703251
nu_norm 5.7739921151070424e-11
Time for iteration 0.7240877151489258 s
------------------ Iteration 15 ------------------
delta_norm 0.0007077769959637994
sigma_norm 0.0004592337403215224
nu_norm 3.1150331615618993e-11
Time for iteration 0.7976510524749756 s