PythonRobotics机器人算法库-FastSLAM1.0
说明:
这是一个使用 FastSLAM 1.0 的基于特征的 SLAM 示例
介绍:

即每个粒子为每个地标保持确定性姿态和 n-EKF,并在每次测量时更新它
粒子最初是从均匀分布中提取的,代表初始不确定性。在每个时间步我们做:
通过使用预测每个粒子的姿势和运动模型(地标未更新)。
用观察更新粒子,其中根据给定传感器测量的粒子具有正确姿势的可能性调整权重
重采样使得权重最大的粒子存活下来,权重最小的粒子消失。
下面的方程式和代码片段我们可以看到粒子分布在我们只提供控制的情况下是如何演变的(), 分别是线速度和角速度。

以下片段回放了每个粒子的记录轨迹。
要了解运动模型,请更改值R并再次重新运行单元格。由于 R 是表示我们对机器人执行运动命令的信任程度的参数。
还值得注意的是,随着粒子开始扩散得更多,只有运动会增加系统的不确定性。如果包括观察结果,不确定性将减少,粒子将收敛到正确的估计
# CODE SNIPPET #
import numpy as np
import math
from copy import deepcopy
# Fast SLAM covariance
Q = np.diag([3.0, np.deg2rad(10.0)])**2
R = np.diag([1.0, np.deg2rad(20.0)])**2
# Simulation parameter
Qsim = np.diag([0.3, np.deg2rad(2.0)])**2
Rsim = np.diag([0.5, np.deg2rad(10.0)])**2
OFFSET_YAWRATE_NOISE = 0.01
DT = 0.1 # time tick [s]
SIM_TIME = 50.0 # simulation time [s]
MAX_RANGE = 20.0 # maximum observation range
M_DIST_TH = 2.0 # Threshold of Mahalanobis distance for data association.
STATE_SIZE = 3 # State size [x,y,yaw]
LM_SIZE = 2 # LM srate size [x,y]
N_PARTICLE = 100 # number of particle
NTH = N_PARTICLE / 1.5 # Number of particle for re-sampling
class Particle:
def __init__(self, N_LM):
self.w = 1.0 / N_PARTICLE
self.x = 0.0
self.y = 0.0
self.yaw = 0.0
# landmark x-y positions
self.lm = np.zeros((N_LM, LM_SIZE))
# landmark position covariance
self.lmP = np.zeros((N_LM * LM_SIZE, LM_SIZE))
def motion_model(x, u):
F = np.array([[1.0, 0, 0],
[0, 1.0, 0],
[0, 0, 1.0]])
B = np.array([[DT * math.cos(x[2, 0]), 0],
[DT * math.sin(x[2, 0]), 0],
[0.0, DT]])
x = F @ x + B @ u
x[2, 0] = pi_2_pi(x[2, 0])
return x
def predict_particles(particles, u):
for i in range(N_PARTICLE):
px = np.zeros((STATE_SIZE, 1))
px[0, 0] = particles[i].x
px[1, 0] = particles[i].y
px[2, 0] = particles[i].yaw
ud = u + (np.random.randn(1, 2) @ R).T # add noise
px = motion_model(px, ud)
particles[i].x = px[0, 0]
particles[i].y = px[1, 0]
particles[i].yaw = px[2, 0]
return particles
def pi_2_pi(angle):
return (angle + math.pi) % (2 * math.pi) - math.pi
# END OF SNIPPET
N_LM = 0
particles = [Particle(N_LM) for i in range(N_PARTICLE)]
time= 0.0
v = 1.0 # [m/s]
yawrate = 0.1 # [rad/s]
u = np.array([v, yawrate]).reshape(2, 1)
history = []
while SIM_TIME >= time:
time += DT
particles = predict_particles(particles, u)
history.append(deepcopy(particles))
# from IPython.html.widgets import *
from ipywidgets import *
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# playback the recorded motion of the particles
def plot_particles(t=0):
x = []
y = []
for i in range(len(history[t])):
x.append(history[t][i].x)
y.append(history[t][i].y)
plt.figtext(0.15,0.82,'t = ' + str(t))
plt.plot(x, y, '.r')
plt.axis([-20,20, -5,25])
interact(plot_particles, t=(0,len(history)-1,1));
interactive(children=(IntSlider(value=0, description='t', max=499), Output()), _dom_classes=('widget-interact'…

# CODE SNIPPET #
def observation(xTrue, xd, u, RFID):
# calc true state
xTrue = motion_model(xTrue, u)
# add noise to range observation
z = np.zeros((3, 0))
for i in range(len(RFID[:, 0])):
dx = RFID[i, 0] - xTrue[0, 0]
dy = RFID[i, 1] - xTrue[1, 0]
d = math.sqrt(dx**2 + dy**2)
angle = pi_2_pi(math.atan2(dy, dx) - xTrue[2, 0])
if d <= MAX_RANGE:
dn = d + np.random.randn() * Qsim[0, 0] # add noise
anglen = angle + np.random.randn() * Qsim[1, 1] # add noise
zi = np.array([dn, pi_2_pi(anglen), i]).reshape(3, 1)
z = np.hstack((z, zi))
# add noise to input
ud1 = u[0, 0] + np.random.randn() * Rsim[0, 0]
ud2 = u[1, 0] + np.random.randn() * Rsim[1, 1] + OFFSET_YAWRATE_NOISE
ud = np.array([ud1, ud2]).reshape(2, 1)
xd = motion_model(xd, ud)
return xTrue, z, xd, ud
def update_with_observation(particles, z):
for iz in range(len(z[0, :])):
lmid = int(z[2, iz])
for ip in range(N_PARTICLE):
# new landmark
if abs(particles[ip].lm[lmid, 0]) <= 0.01:
particles[ip] = add_new_lm(particles[ip], z[:, iz], Q)
# known landmark
else:
w = compute_weight(particles[ip], z[:, iz], Q)
particles[ip].w *= w
particles[ip] = update_landmark(particles[ip], z[:, iz], Q)
return particles
def compute_weight(particle, z, Q):
lm_id = int(z[2])
xf = np.array(particle.lm[lm_id, :]).reshape(2, 1)
Pf = np.array(particle.lmP[2 * lm_id:2 * lm_id + 2])
zp, Hv, Hf, Sf = compute_jacobians(particle, xf, Pf, Q)
dx = z[0:2].reshape(2, 1) - zp
dx[1, 0] = pi_2_pi(dx[1, 0])
try:
invS = np.linalg.inv(Sf)
except np.linalg.linalg.LinAlgError:
print("singuler")
return 1.0
num = math.exp(-0.5 * dx.T @ invS @ dx)
den = 2.0 * math.pi * math.sqrt(np.linalg.det(Sf))
w = num / den
return w
def compute_jacobians(particle, xf, Pf, Q):
dx = xf[0, 0] - particle.x
dy = xf[1, 0] - particle.y
d2 = dx**2 + dy**2
d = math.sqrt(d2)
zp = np.array(
[d, pi_2_pi(math.atan2(dy, dx) - particle.yaw)]).reshape(2, 1)
Hv = np.array([[-dx / d, -dy / d, 0.0],
[dy / d2, -dx / d2, -1.0]])
Hf = np.array([[dx / d, dy / d],
[-dy / d2, dx / d2]])
Sf = Hf @ Pf @ Hf.T + Q
return zp, Hv, Hf, Sf
def add_new_lm(particle, z, Q):
r = z[0]
b = z[1]
lm_id = int(z[2])
s = math.sin(pi_2_pi(particle.yaw + b))
c = math.cos(pi_2_pi(particle.yaw + b))
particle.lm[lm_id, 0] = particle.x + r * c
particle.lm[lm_id, 1] = particle.y + r * s
# covariance
Gz = np.array([[c, -r * s],
[s, r * c]])
particle.lmP[2 * lm_id:2 * lm_id + 2] = Gz @ Q @ Gz.T
return particle
def update_KF_with_cholesky(xf, Pf, v, Q, Hf):
PHt = Pf @ Hf.T
S = Hf @ PHt + Q
S = (S + S.T) * 0.5
SChol = np.linalg.cholesky(S).T
SCholInv = np.linalg.inv(SChol)
W1 = PHt @ SCholInv
W = W1 @ SCholInv.T
x = xf + W @ v
P = Pf - W1 @ W1.T
return x, P
def update_landmark(particle, z, Q):
lm_id = int(z[2])
xf = np.array(particle.lm[lm_id, :]).reshape(2, 1)
Pf = np.array(particle.lmP[2 * lm_id:2 * lm_id + 2, :])
zp, Hv, Hf, Sf = compute_jacobians(particle, xf, Pf, Q)
dz = z[0:2].reshape(2, 1) - zp
dz[1, 0] = pi_2_pi(dz[1, 0])
xf, Pf = update_KF_with_cholesky(xf, Pf, dz, Q, Hf)
particle.lm[lm_id, :] = xf.T
particle.lmP[2 * lm_id:2 * lm_id + 2, :] = Pf
return particle
# END OF CODE SNIPPET #
# Setting up the landmarks
RFID = np.array([[10.0, -2.0],
[15.0, 10.0]])
N_LM = RFID.shape[0]
# Initialize 1 particle
N_PARTICLE = 1
particles = [Particle(N_LM) for i in range(N_PARTICLE)]
xTrue = np.zeros((STATE_SIZE, 1))
xDR = np.zeros((STATE_SIZE, 1))
print("initial weight", particles[0].w)
xTrue, z, _, ud = observation(xTrue, xDR, u, RFID)
# Initialize landmarks
particles = update_with_observation(particles, z)
print("weight after landmark intialization", particles[0].w)
particles = update_with_observation(particles, z)
print("weight after update ", particles[0].w)
particles[0].x = -10
particles = update_with_observation(particles, z)
print("weight after wrong prediction", particles[0].w)
initial weight 1.0
weight after landmark intialization 1.0
weight after update 0.023098460073039763
weight after wrong prediction 7.951154575772496e-07

# CODE SNIPPET #
def normalize_weight(particles):
sumw = sum([p.w for p in particles])
try:
for i in range(N_PARTICLE):
particles[i].w /= sumw
except ZeroDivisionError:
for i in range(N_PARTICLE):
particles[i].w = 1.0 / N_PARTICLE
return particles
return particles
def resampling(particles):
"""
low variance re-sampling
"""
particles = normalize_weight(particles)
pw = []
for i in range(N_PARTICLE):
pw.append(particles[i].w)
pw = np.array(pw)
Neff = 1.0 / (pw @ pw.T) # Effective particle number
# print(Neff)
if Neff < NTH: # resampling
wcum = np.cumsum(pw)
base = np.cumsum(pw * 0.0 + 1 / N_PARTICLE) - 1 / N_PARTICLE
resampleid = base + np.random.rand(base.shape[0]) / N_PARTICLE
inds = []
ind = 0
for ip in range(N_PARTICLE):
while ((ind < wcum.shape[0] - 1) and (resampleid[ip] > wcum[ind])):
ind += 1
inds.append(ind)
tparticles = particles[:]
for i in range(len(inds)):
particles[i].x = tparticles[inds[i]].x
particles[i].y = tparticles[inds[i]].y
particles[i].yaw = tparticles[inds[i]].yaw
particles[i].w = 1.0 / N_PARTICLE
return particles, inds
# END OF SNIPPET #
def gaussian(x, mu, sig):
return np.exp(-np.power(x - mu, 2.) / (2 * np.power(sig, 2.)))
N_PARTICLE = 100
particles = [Particle(N_LM) for i in range(N_PARTICLE)]
x_pos = []
w = []
for i in range(N_PARTICLE):
particles[i].x = np.linspace(-0.5,0.5,N_PARTICLE)[i]
x_pos.append(particles[i].x)
particles[i].w = gaussian(i, N_PARTICLE/2, N_PARTICLE/20)
w.append(particles[i].w)
# Normalize weights
sw = sum(w)
for i in range(N_PARTICLE):
w[i] /= sw
particles, new_indices = resampling(particles)
x_pos2 = []
for i in range(N_PARTICLE):
x_pos2.append(particles[i].x)
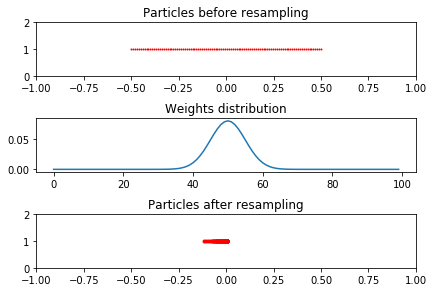
# Plot results
fig, ((ax1,ax2,ax3)) = plt.subplots(nrows=3, ncols=1)
fig.tight_layout()
ax1.plot(x_pos,np.ones((N_PARTICLE,1)), '.r', markersize=2)
ax1.set_title("Particles before resampling")
ax1.axis((-1, 1, 0, 2))
ax2.plot(w)
ax2.set_title("Weights distribution")
ax3.plot(x_pos2,np.ones((N_PARTICLE,1)), '.r')
ax3.set_title("Particles after resampling")
ax3.axis((-1, 1, 0, 2))
fig.subplots_adjust(hspace=0.8)
plt.show()
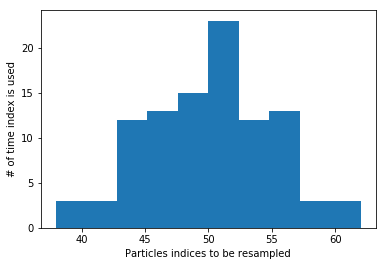
plt.figure()
plt.hist(new_indices)
plt.xlabel("Particles indices to be resampled")
plt.ylabel("# of time index is used")
plt.show()
进入目录PythonRobotics/SLAM/FastSLAM1
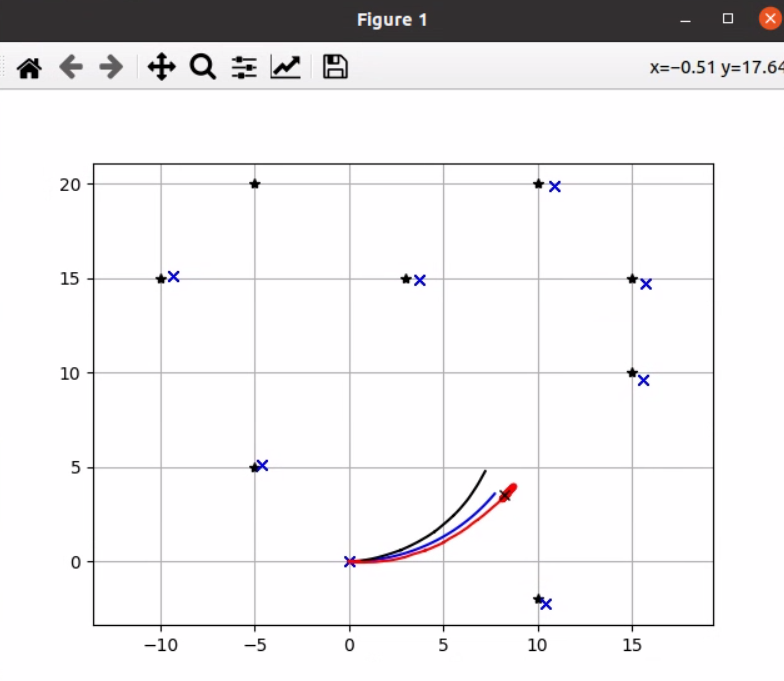
执行文件
python3 fast_slam1.py
- 结果如下
获取最新文章: 扫一扫右上角的二维码加入“创客智造”公众号



















