无人驾驶汽车系统入门(三)——无损卡尔曼滤波,目标追踪,C++
无人驾驶汽车系统入门(三)——无损卡尔曼滤波,目标追踪,C++
说明:
- 介绍前面两篇文章我们了解了卡尔曼滤波以及扩展卡尔曼滤波在目标追踪的应用,我们在上一篇文章中还具体用Python实现了EKF,但是细心的同学会发现,EKF的效率确实很低,计算雅可比矩阵确实是一个很费时的操作,当问题(非线性的)一旦变得复杂,其计算量就变得十分不可控制。在此再向大家接受一种滤波——无损卡尔曼滤波(Unscented Kalman Filter, UKF)
UKF
通过上一篇文章,我们已经知道KF不适用于非线性系统,为处理非线性系统,我们通过一阶泰勒展式来近似(用线性函数近似)
这个方案直接的结果就是,我们对于具体的问题都要求解对应的一阶偏导(雅可比矩阵),求解雅可比矩阵本身就是费时的计算,而且我们上一篇还使用了Python而非C++,而且我们图省事还用了一个叫做numdifftools的库来实现雅可比矩阵的求解而不是自行推导,这一切都造成了我们上一次博客的代码执行效率奇低!
显然现实应用里面我们的无人车是不能接受这种延迟的,我相信很多同学也和我一样讨厌求解雅可比矩阵,那么,就让我们来学习一种相对简单的状态估计算法——UKF。
UKF使用的是统计线性化技术,我们把这种线性化的方法叫做无损变换(unscented transformation)这一技术主要通过n个在先验分布中采集的点(我们把它们叫sigma points)的线性回归来线性化随机变量的非线性函数
由于我们考虑的是随机变量的扩展,所以这种线性化要比泰勒级数线性化(EKF所使用的策略)更准确。
和EKF一样,UKF也主要分为预测和更新。
运动模型

非线性处理/测量模型
我们知道我们在应用KF是面临的主要问题就是非线性处理模型(比如说CTRV)和非线性测量模型(RADAR测量)的处理。
我们从概率分布的角度来描述这个问题:

UKF的基本思路就是: 近似非线性函数的概率分布要比近似非线性函数本身要容易!
那么如何去找一个与真实分布近似的高斯分布呢?——找一个与真实分布有着相同的均值和协方差的高斯分布。
那么如何去找这样的均值和方差呢?——无损变换。
无损变换
- 计算一堆点(术语叫做sigma point),通过一定的手段产生的这些sigma点能够代表当前的分布,
- 然后将这些点通过非线性函数(处理模型)变换成一些新的点,
- 然后基于这些新的sigma点计算出一个高斯分布(带有权重地计算出来)如图:
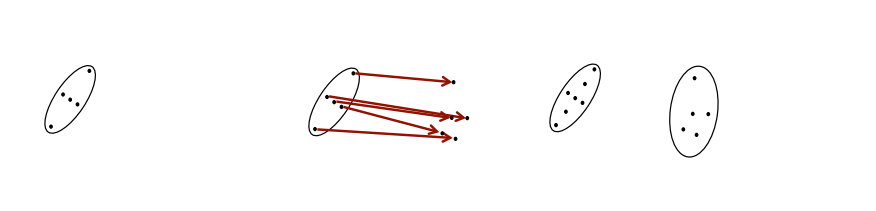
预测
- 由一个高斯分布产生sigma point
- 通常,假定状态的个数为 n ,我们会产生 2n+1 个sigma点,
- 其中第一个就是我们当前状态的均值 μ ,sigma点集的均值的计算公式为:


预测sigma point

预测均值和方差

测量更新
1.预测测量(将先验映射到测量空间然后算出均值和方差)
- 这篇博客继续使用上一篇(EKF)中的测量实验数据,那么我们知道,测量更新分为两个部分,LIDAR测量和RADAR测量,
- 其中LIDAR测量模型本身就是线性的,所以我们重点还是放在RADAR测量模型的处理上面,RADAR的测量映射函数为:


2.更新状态

- http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.136.6539&rep=rep1&type=pdf
- https://www.cse.sc.edu/~terejanu/files/tutorialUKF.pdf
- http://ais.informatik.uni-freiburg.de/teaching/ws13/mapping/pdf/slam06-ukf-4.pdf
UKF实例
- 我们继续基于上一篇文章的数据来做状态估计的实例,不过,为了更加接近实际实际的应用,我们本节采用C++实现。
- 由于本节使用的C++代码量相对较大,而且为多文件的项目,代码就不再一一贴出,所有代码我都已经上传至如下地址:
- http://download.csdn.net/download/adamshan/10041096
- 运行-效果
- 首先解压,编译:
mkdir build
cd build
cmake ..
make
- 运行:
./ukf ../data/data_synthetic.txt ../data/output.txt
- 得到计算的结果:
Accuracy - RMSE:
0.0723408
0.0821208
0.342265
0.23017
- 我们发现,这个UKF要比我们上一篇博客写的EKF的效率要高得多得多。
- 我们执行可视化的python脚本看一下效果:
cd ../data
python plot.py
- 得到如下结果:
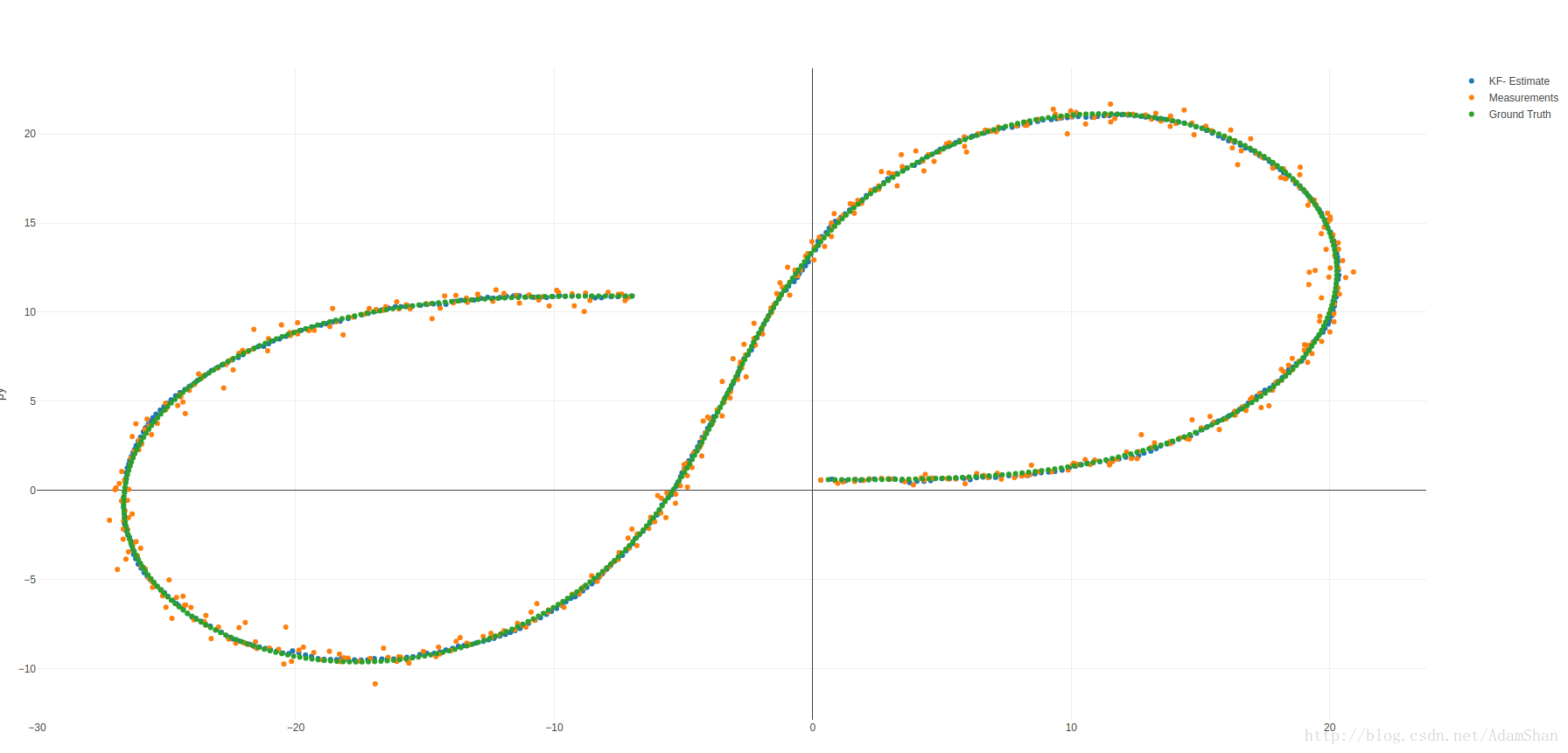
- 放大一点:
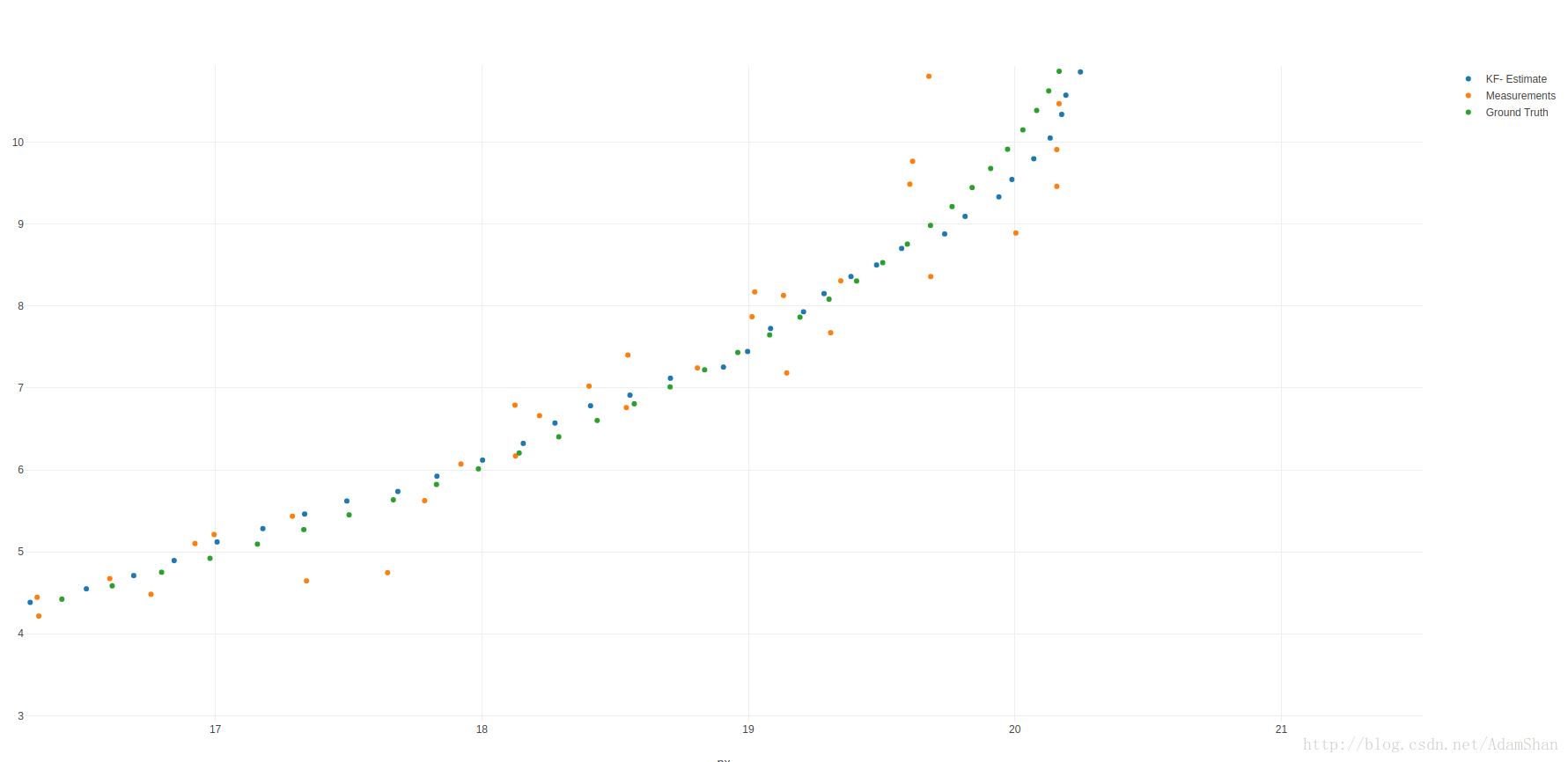
- UKF在我们这个问题中的执行效率和估计精度都高于我们上一篇文章中实现的EKF,下面就让我们看一下核心代码。
核心代码
- 首先是预测,预测主要包含三部分,分别是:
- 产生sigma点集
- 基于CTRV模型预测sigma点集
- 计算新的均值核方差
- 产生sigma点集
void UKF::AugmentedSigmaPoints(MatrixXd *Xsig_out) {
//create augmented mean vector
VectorXd x_aug = VectorXd(7);
//create augmented state covariance
MatrixXd P_aug = MatrixXd(7, 7);
//create sigma point matrix
MatrixXd Xsig_aug = MatrixXd(n_aug_, 2 * n_aug_ + 1);
//create augmented mean state
//create augmented covariance matrix
//create square root matrix
//create augmented sigma points
x_aug.head(5) = x_;
x_aug(5) = 0;
x_aug(6) = 0;
P_aug.fill(0.0);
P_aug.topLeftCorner(5, 5) = P_;
P_aug(5,5) = std_a_*std_a_;
P_aug(6,6) = std_yawdd_*std_yawdd_;
MatrixXd A = P_aug.llt().matrixL();
//create augmented sigma points
Xsig_aug.col(0) = x_aug;
for (int i = 0; i< n_aug_; i++)
{
Xsig_aug.col(i+1) = x_aug + sqrt(lambda_+n_aug_) * A.col(i);
Xsig_aug.col(i+1+n_aug_) = x_aug - sqrt(lambda_+n_aug_) * A.col(i);
}
//write result
*Xsig_out = Xsig_aug;
}
2.基于CTRV模型预测sigma点集
void UKF::SigmaPointPrediction(MatrixXd &Xsig_aug, double delta_t) {
for(int i =0; i < (2 * n_aug_ + 1); i++){
VectorXd input_x = Xsig_aug.col(i);
float px = input_x[0];
float py = input_x[1];
float v = input_x[2];
float psi = input_x[3];
float psi_dot = input_x[4];
float mu_a = input_x[5];
float mu_psi_dot_dot = input_x[6];
VectorXd term2 = VectorXd(5);
VectorXd term3 = VectorXd(5);
VectorXd result = VectorXd(5);
if(psi_dot < 0.001){
term2 << v * cos(psi) * delta_t, v * sin(psi) * delta_t, 0, psi_dot * delta_t, 0;
term3 << 0.5 * delta_t*delta_t * cos(psi) * mu_a,
0.5 * delta_t*delta_t * sin(psi) * mu_a,
delta_t * mu_a,
0.5 * delta_t*delta_t * mu_psi_dot_dot,
delta_t * mu_psi_dot_dot;
result = Xsig_aug.col(i).head(5) + term2 + term3;
} else{
term2 << (v/psi_dot) * (sin(psi + psi_dot * delta_t) - sin(psi)),
(v/psi_dot) * (-cos(psi + psi_dot * delta_t) + cos(psi)),
0,
psi_dot * delta_t,
0;
term3 << 0.5 * delta_t*delta_t * cos(psi) * mu_a,
0.5 * delta_t*delta_t * sin(psi) * mu_a,
delta_t * mu_a,
0.5 * delta_t*delta_t * mu_psi_dot_dot,
delta_t * mu_psi_dot_dot;
result = Xsig_aug.col(i).head(5) + term2 + term3;
}
Xsig_pred_.col(i) = result;
}
}
3.计算新的均值核方差
void UKF::PredictMeanAndCovariance() {
x_.fill(0.0);
for(int i=0; i<2*n_aug_+1; i++){
x_ = x_+ weights_[i] * Xsig_pred_.col(i);
}
P_.fill(0.0);
for(int i=0; i<2*n_aug_+1; i++){
VectorXd x_diff = Xsig_pred_.col(i) - x_;
while (x_diff[3]> M_PI)
x_diff[3] -= 2.*M_PI;
while (x_diff[3] <-M_PI)
x_diff[3]+=2.*M_PI;
P_ = P_ + weights_[i] * x_diff * x_diff.transpose();
}
}
测量更新主要分为
- 预测LIDAR测量
- 预测RADAR测量
- 更新状态
- 预测LIDAR测量
void UKF::PredictLaserMeasurement(VectorXd &z_pred, MatrixXd &S, MatrixXd &Zsig, long n_z) {
for(int i=0; i < 2*n_aug_+1; i++){
float px = Xsig_pred_.col(i)[0];
float py = Xsig_pred_.col(i)[1];
VectorXd temp = VectorXd(n_z);
temp << px, py;
Zsig.col(i) = temp;
}
z_pred.fill(0.0);
for(int i=0; i < 2*n_aug_+1; i++){
z_pred = z_pred + weights_[i] * Zsig.col(i);
}
S.fill(0.0);
for(int i=0; i < 2*n_aug_+1; i++){
//residual
VectorXd z_diff = Zsig.col(i) - z_pred;
S = S + weights_[i] * z_diff * z_diff.transpose();
}
S = S + R_laser_;
}
- 预测RADAR测量
void UKF::PredictRadarMeasurement(VectorXd &z_pred, MatrixXd &S, MatrixXd &Zsig, long n_z) {
for(int i=0; i < 2*n_aug_+1; i++){
float px = Xsig_pred_.col(i)[0];
float py = Xsig_pred_.col(i)[1];
float v = Xsig_pred_.col(i)[2];
float psi = Xsig_pred_.col(i)[3];
float psi_dot = Xsig_pred_.col(i)[4];
float temp = px * px + py * py;
float rho = sqrt(temp);
float phi = atan2(py, px);
float rho_dot;
if(fabs(rho) < 0.0001){
rho_dot = 0;
} else{
rho_dot =(px * cos(psi) * v + py * sin(psi) * v)/rho;
}
VectorXd temp1 = VectorXd(3);
temp1 << rho, phi, rho_dot;
Zsig.col(i) = temp1;
}
z_pred.fill(0.0);
for(int i=0; i < 2*n_aug_+1; i++){
z_pred = z_pred + weights_[i] * Zsig.col(i);
}
S.fill(0.0);
for(int i=0; i < 2*n_aug_+1; i++){
//residual
VectorXd z_diff = Zsig.col(i) - z_pred;
//angle normalization
while (z_diff(1)> M_PI) z_diff(1)-=2.*M_PI;
while (z_diff(1)<-M_PI) z_diff(1)+=2.*M_PI;
S = S + weights_[i] * (Zsig.col(i) - z_pred) * (Zsig.col(i) - z_pred).transpose();
}
S = S + R_radar_;
}
3.更新状态
void UKF::UpdateState(VectorXd &z, VectorXd &z_pred, MatrixXd &S, MatrixXd &Zsig, long n_z) {
//create matrix for cross correlation Tc
MatrixXd Tc = MatrixXd(n_x_, n_z);
//calculate cross correlation matrix
//calculate Kalman gain K;
//update state mean and covariance matrix
Tc.fill(0.0);
for(int i=0; i < 2*n_aug_+1; i++){
VectorXd x_diff = Xsig_pred_.col(i) - x_;
while (x_diff(3)> M_PI) x_diff(3)-=2.*M_PI;
while (x_diff(3)<-M_PI) x_diff(3)+=2.*M_PI;
//residual
VectorXd z_diff = Zsig.col(i) - z_pred;
if(n_z == 3){
//angle normalization
while (z_diff(1)> M_PI) z_diff(1)-=2.*M_PI;
while (z_diff(1)<-M_PI) z_diff(1)+=2.*M_PI;
}
Tc = Tc + weights_[i] * x_diff * z_diff.transpose();
}
MatrixXd K = MatrixXd(5, 3);
K = Tc * S.inverse();
VectorXd y = z - z_pred;
//angle normalization
if(n_z == 3){
while (y(1)> M_PI) y(1)-=2.*M_PI;
while (y(1)<-M_PI) y(1)+=2.*M_PI;
}
x_ = x_ + K * y;
P_ = P_ - K * S * K.transpose();
}
- 以上就是我们的UKF的核心算法实现了,可能光看这些核心代码还是没办法理解,所以感兴趣的童鞋就去下载来再详细研究把~
- 上一篇文章我买了个关子,没有贴出把结果可视化的代码,本次代码已经一本包含在项目里(具体见/data/plot.py)
- 前面三篇文章都介绍了卡尔曼滤波相关的算法,大家应该已经看出卡尔曼滤波这类贝叶斯滤波器在无人驾驶汽车系统哦的重要性了,卡尔曼滤波作为重要的状态估计算法,是无人驾驶的必备技能点,所以相关的扩展阅读大家可以多多开展,
- 本系列暂时就不再讨论了,下面我想向大家介绍应用于无人驾驶中的控制算法,控制作为自动化中重要的技术,有着很多的分支,后面的文章我会继续由理论到实践逐一向大家介绍相关技术~
参考:
- https://blog.csdn.net/AdamShan/article/details/78359048
获取最新文章: 扫一扫右上角的二维码加入“创客智造”公众号



















