< >
Home » 无人驾驶汽车系统入门 » 无人驾驶汽车系统入门（二）——高级运动模型和扩展卡尔曼滤波

无人驾驶汽车系统入门（二）——高级运动模型和扩展卡尔曼滤波

无人驾驶汽车系统入门（二）——高级运动模型和扩展卡尔曼滤波

说明：

  • 介绍高级运动模型和扩展卡尔曼滤波

前言：

  • 上一篇文章的最后我们提到卡尔曼滤波存在着一个非常大的局限性——它仅能对线性的处理模型和测量模型进行精确的估计，在非线性的场景中并不能达到最优的估计效果。
  • 所以之前为了保证我们的处理模型是线性的，我们上一节中使用了恒定速度模型，然后将估计目标的加减速用处理噪声来表示，这一模型用来估算行人的状态其实已经足够了
  • 但是在现实的驾驶环境中，我们不仅要估计行人，我们除了估计行人状态以外，我们还需要估计其他车辆，自行车等等状态，他们的状态估计显然不能使用简单的线性系统来描述
  • 这里，我们介绍非线性系统情况下的一种广泛使用的滤波算法——扩展卡尔曼滤波(Extended Kalman Filter, EKF)
  • 本节讲解非线性系统中广泛使用的扩展卡尔曼滤波算法，我们通常将该算法应用于实际的车辆状态估计（或者说车辆追踪）中。
  • 另外，实际的车辆追踪运动模型显然不能使用简单的恒定速度模型来建模
  • 在本节中会介绍几种应用于车辆追踪的高级运动模型。
  • 并且已经其中的CTRV模型来构造我们的扩展卡尔曼滤波。
  • 最后，在代码实例中，我会介绍如何使用EKF做多传感器融合。

应用于车辆追踪的高级运动模型

  • 首先要明确的一点是，不管是什么运动模型，本质上都是为了帮助我们简化问题，所以我们可以根据运动模型的复杂程度（次数）来给我们常用的运动模型分一下类。
  1. 一次运动模型（也别称为线性运动模型）：
  • 恒定速度模型（Constant Velocity, CV）
  • 恒定加速度模型（Constant Acceleration, CA）
  • 这些线性运动模型假定目标是直线运动的，并不考虑物体的转弯。
  1. 二次运动模型：
  • 恒定转率和速度模型（Constant Turn Rate and Velocity，CTRV）
  • 恒定转率和加速度模型（Constant Turn Rate and Acceleration，CTRA）
  1. CTRV

  • CTRV目前多用于机载追踪系统（飞机），这些二次运动模型大多假定速度 vv 和 偏航角速度（yaw rate） ωω 没有关系，因此，在这类运动模型中，由于偏航角速度测量的扰动（不稳定），即使车辆没有移动，我们的运动模型下的角速度也会发生细微的变化。

  • 为了解决这个问题，速度 vv 和 偏航角速度 ωω 的关联可以通过设定转向角 ΦΦ 恒定来建立，这样就引出了 恒定转向角和速度模型（Constant Steering Angle and Velocity，CSAV）, 另外，速度可以别假定为线性变化的，进而引出了常曲率和加速度模型（Constant Curvature and Acceleration，CCA）。

  • 这些运动模型的关系如图：
    请输入图片描述

运动模型的状态转移公式

  • 由于除CCA以外，以上的运动模型都非常著名，故本文不提供详细的推导过程。本文提供CV和CTRV模型的状态转移公式。
  • 状态转移公式：就是我们的处理模型由上一状态的估计计算下一个状态的先验分布的计算公式，可以理解为我们基于一定的先验
  • 知识总结出来的运动公式。

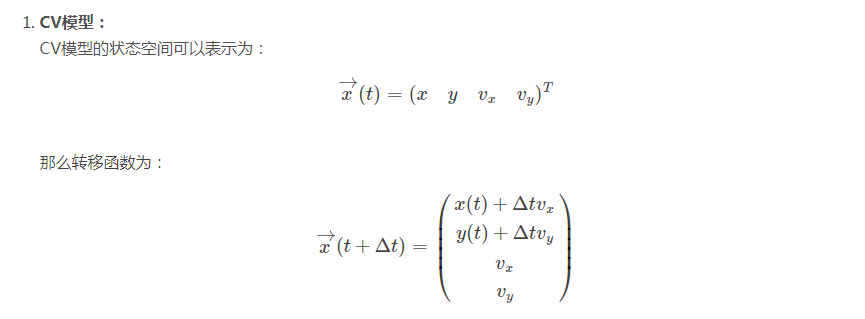
请输入图片描述

请输入图片描述

请输入图片描述

  • 扩展卡尔曼滤波
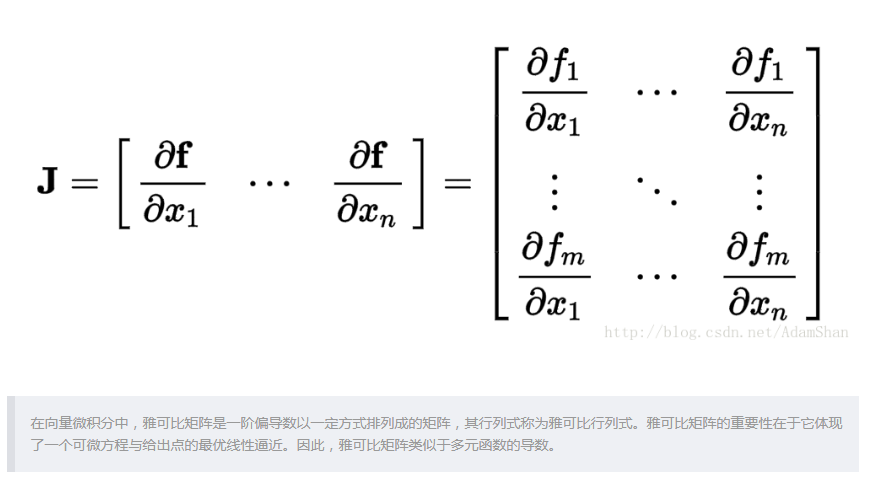
  1. 雅可比矩阵

请输入图片描述

请输入图片描述

请输入图片描述

请输入图片描述

请输入图片描述

  1. 处理噪声

请输入图片描述

请输入图片描述

请输入图片描述

  1. 测量

请输入图片描述

将预测映射到激光雷达测量空间：

请输入图片描述

虽然这个雅可比矩阵看似非常复杂，但是我们待会编程的时候并不需要完整的推导出这个雅可比矩阵的表达式，在本篇中，我们采用numdifftools这个公式来直接求解雅可比矩阵。

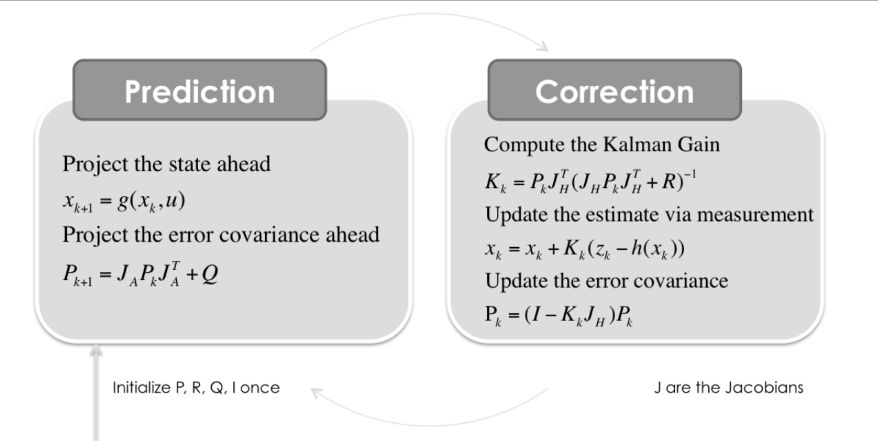
综上，EKF的整个过程为：

请输入图片描述

4.Python实现

  • 和之前一样，为了实现交互式的代码，实例的代码为了便于理解，我们仍然使用大家熟悉的Python来实现
  • 当然，实际无人车项目肯定是需要用C++来实现的，要将下面的示例代码使用C++来改写是非常简单快速的。
  • 首先引入相关的库：
from __future__ import print_function
import numpy as np
import matplotlib.dates as mdates
import matplotlib.pyplot as plt
from scipy.stats import norm
from sympy import Symbol, symbols, Matrix, sin, cos, sqrt, atan2
from sympy import init_printing
init_printing(use_latex=True)
import numdifftools as nd
import math
  • 首先我们读取我们的数据集，该数据集包含了追踪目标的LIDAR和RADAR的测量值，以及测量的时间点
  • 同时为了验证我们追踪目标的精度，该数据还包含了追踪目标的真实坐标。（数据下载链接见文章末尾）

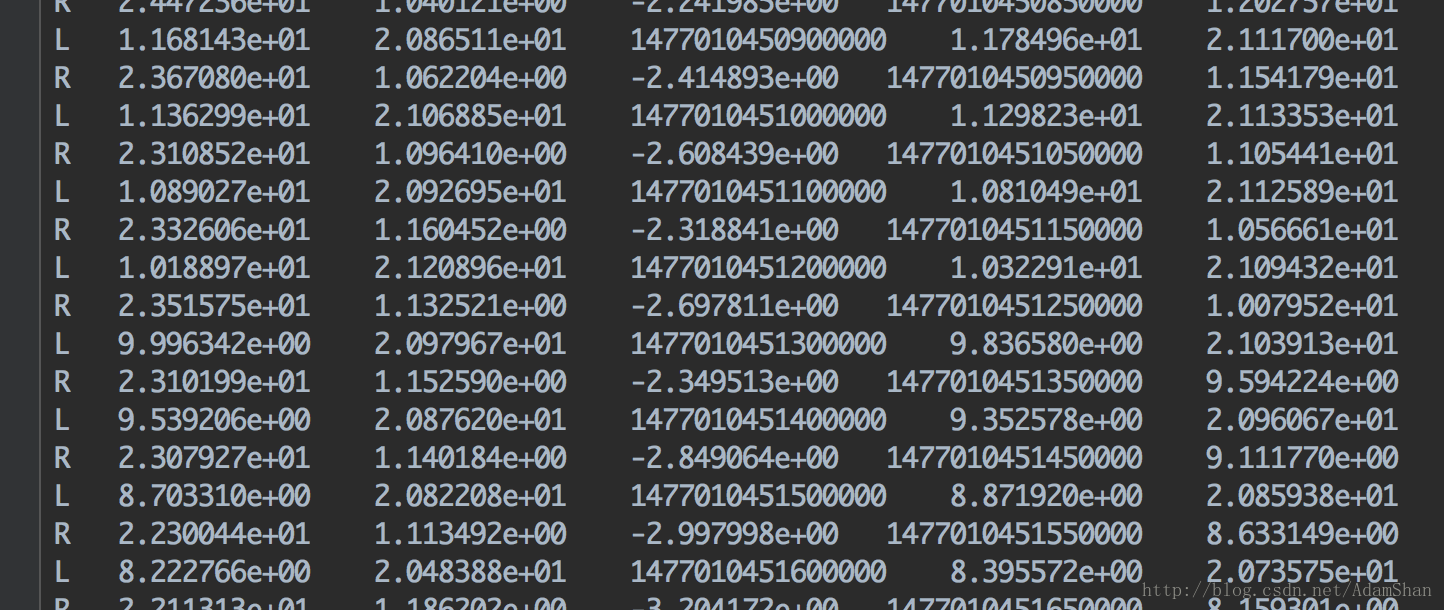
请输入图片描述

  • 其中第一列表示测量数据来自LIDAR还是RADAR，LIDAR的2，3列表示测量的目标 (x,y)(x,y),第4列表示测量的时间点，第5，6，7，8表示真实的(x,y,vx,vy)(x,y,vx,vy), RADAR测量的(前三列)是(ρ,ψ,ρ˙)(ρ,ψ,ρ˙)，其余列的数据的意义和LIDAR一样。

  • 首先我们读取整个数据：

dataset = []

# read the measurement data, use 0.0 to stand LIDAR data
# and 1.0 stand RADAR data
with open('data_synthetic.txt', 'rb') as f:
    lines = f.readlines()
    for line in lines:
        line = line.strip('\n')
        line = line.strip()
        numbers = line.split()
        result = []
        for i, item in enumerate(numbers):
            item.strip()
            if i == 0:
                if item == 'L':
                    result.append(0.0)
                else:
                    result.append(1.0)
            else:
                result.append(float(item))
        dataset.append(result)
    f.close()

请输入图片描述

P = np.diag([1.0, 1.0, 1.0, 1.0, 1.0])
print(P, P.shape)
H_lidar = np.array([[ 1.,  0.,  0.,  0.,  0.],
       [ 0.,  1.,  0.,  0.,  0.]])
print(H_lidar, H_lidar.shape)

R_lidar = np.array([[0.0225, 0.],[0., 0.0225]])
R_radar = np.array([[0.09, 0., 0.],[0., 0.0009, 0.], [0., 0., 0.09]])
print(R_lidar, R_lidar.shape)
print(R_radar, R_radar.shape)

# process noise standard deviation for a
std_noise_a = 2.0
# process noise standard deviation for yaw acceleration
std_noise_yaw_dd = 0.3
  • 在整个预测和测量更新过程中，所有角度量的数值都应该控制在 [−π,π]，我们知道角度加减 2π 不变，
  • 所以用如下函数表示函数来调整角度：
def control_psi(psi):
    while (psi > np.pi or psi < -np.pi):
        if psi > np.pi:
            psi = psi - 2 * np.pi
        if psi < -np.pi:
            psi = psi + 2 * np.pi
    return psi

请输入图片描述

  • 具体状态初始化代码为：
state = np.zeros(5)
init_measurement = dataset[0]
current_time = 0.0
if init_measurement[0] == 0.0:
    print('Initialize with LIDAR measurement!')
    current_time = init_measurement[3]
    state[0] = init_measurement[1]
    state[1] = init_measurement[2]

else:
    print('Initialize with RADAR measurement!')
    current_time = init_measurement[4]
    init_rho = init_measurement[1]
    init_psi = init_measurement[2]
    init_psi = control_psi(init_psi)
    state[0] = init_rho * np.cos(init_psi)
    state[1] = init_rho * np.sin(init_psi)
print(state, state.shape)
  • 写一个辅助函数用于保存数值：
# Preallocation for Saving
px = []
py = []
vx = []
vy = []

gpx = []
gpy = []
gvx = []
gvy = []

mx = []
my = []

def savestates(ss, gx, gy, gv1, gv2, m1, m2):
    px.append(ss[0])
    py.append(ss[1])
    vx.append(np.cos(ss[3]) * ss[2])
    vy.append(np.sin(ss[3]) * ss[2])

    gpx.append(gx)
    gpy.append(gy)
    gvx.append(gv1)
    gvy.append(gv2)
    mx.append(m1)
    my.append(m2)
  • 定义状态转移函数和测量函数，使用numdifftools库来计算其对应的雅可比矩阵，
  • 这里我们先设 Δt=0.05，只是为了占一个位置，当实际运行EKF时会计算出前后两次测量的时间差，一次来替换这里的 Δt。
measurement_step = len(dataset)
state = state.reshape([5, 1])
dt = 0.05

I = np.eye(5)

transition_function = lambda y: np.vstack((
    y[0] + (y[2] / y[4]) * (np.sin(y[3] + y[4] * dt) - np.sin(y[3])),
    y[1] + (y[2] / y[4]) * (-np.cos(y[3] + y[4] * dt) + np.cos(y[3])),
    y[2],
    y[3] + y[4] * dt,
    y[4]))

# when omega is 0
transition_function_1 = lambda m: np.vstack((m[0] + m[2] * np.cos(m[3]) * dt,
                                             m[1] + m[2] * np.sin(m[3]) * dt,
                                             m[2],
                                             m[3] + m[4] * dt,
                                             m[4]))

J_A = nd.Jacobian(transition_function)
J_A_1 = nd.Jacobian(transition_function_1)
# print(J_A([1., 2., 3., 4., 5.]))

measurement_function = lambda k: np.vstack((np.sqrt(k[0] * k[0] + k[1] * k[1]),
                                            math.atan2(k[1], k[0]),
                                            (k[0] * k[2] * np.cos(k[3]) + k[1] * k[2] * np.sin(k[3])) / np.sqrt(k[0] * k[0] + k[1] * k[1])))
J_H = nd.Jacobian(measurement_function)
# J_H([1., 2., 3., 4., 5.])
  • EKF的过程代码：
for step in range(1, measurement_step):

    # Prediction
    # ========================
    t_measurement = dataset[step]
    if t_measurement[0] == 0.0:
        m_x = t_measurement[1]
        m_y = t_measurement[2]
        z = np.array([[m_x], [m_y]])

        dt = (t_measurement[3] - current_time) / 1000000.0
        current_time = t_measurement[3]

        # true position
        g_x = t_measurement[4]
        g_y = t_measurement[5]
        g_v_x = t_measurement[6]
        g_v_y = t_measurement[7]

    else:
        m_rho = t_measurement[1]
        m_psi = t_measurement[2]
        m_dot_rho = t_measurement[3]
        z = np.array([[m_rho], [m_psi], [m_dot_rho]])

        dt = (t_measurement[4] - current_time) / 1000000.0
        current_time = t_measurement[4]

        # true position
        g_x = t_measurement[5]
        g_y = t_measurement[6]
        g_v_x = t_measurement[7]
        g_v_y = t_measurement[8]

    if np.abs(state[4, 0]) < 0.0001:  # omega is 0, Driving straight
        state = transition_function_1(state.ravel().tolist())
        state[3, 0] = control_psi(state[3, 0])
        JA = J_A_1(state.ravel().tolist())
    else:  # otherwise
        state = transition_function(state.ravel().tolist())
        state[3, 0] = control_psi(state[3, 0])
        JA = J_A(state.ravel().tolist())


    G = np.zeros([5, 2])
    G[0, 0] = 0.5 * dt * dt * np.cos(state[3, 0])
    G[1, 0] = 0.5 * dt * dt * np.sin(state[3, 0])
    G[2, 0] = dt
    G[3, 1] = 0.5 * dt * dt
    G[4, 1] = dt

    Q_v = np.diag([std_noise_a*std_noise_a, std_noise_yaw_dd*std_noise_yaw_dd])
    Q = np.dot(np.dot(G, Q_v), G.T)

    # Project the error covariance ahead
    P = np.dot(np.dot(JA, P), JA.T) + Q

    # Measurement Update (Correction)
    # ===============================
    if t_measurement[0] == 0.0:
        # Lidar
        S = np.dot(np.dot(H_lidar, P), H_lidar.T) + R_lidar
        K = np.dot(np.dot(P, H_lidar.T), np.linalg.inv(S))

        y = z - np.dot(H_lidar, state)
        y[1, 0] = control_psi(y[1, 0])
        state = state + np.dot(K, y)
        state[3, 0] = control_psi(state[3, 0])
        # Update the error covariance
        P = np.dot((I - np.dot(K, H_lidar)), P)

        # Save states for Plotting
        savestates(state.ravel().tolist(), g_x, g_y, g_v_x, g_v_y, m_x, m_y)

    else:
        # Radar
        JH = J_H(state.ravel().tolist())

        S = np.dot(np.dot(JH, P), JH.T) + R_radar
        K = np.dot(np.dot(P, JH.T), np.linalg.inv(S))
        map_pred = measurement_function(state.ravel().tolist())
        if np.abs(map_pred[0, 0]) < 0.0001:
            # if rho is 0
            map_pred[2, 0] = 0

        y = z - map_pred
        y[1, 0] = control_psi(y[1, 0])

        state = state + np.dot(K, y)
        state[3, 0] = control_psi(state[3, 0])
        # Update the error covariance
        P = np.dot((I - np.dot(K, JH)), P)

        savestates(state.ravel().tolist(), g_x, g_y, g_v_x, g_v_y, m_rho * np.cos(m_psi), m_rho * np.sin(m_psi))
  • 这里有几点需要注意，首先，要考虑清楚有几个地方被除数有可能为 0，比如说ω=0，以及 ρ=0 的情况。
  • 处理完以后我们输出估计的均方误差（RMSE），并且把各类数据保存以便我们可视化我们的EKF的效果：
def rmse(estimates, actual):
    result = np.sqrt(np.mean((estimates-actual)**2))
    return result

print(rmse(np.array(px), np.array(gpx)),
      rmse(np.array(py), np.array(gpy)),
      rmse(np.array(vx), np.array(gvx)),
      rmse(np.array(vy), np.array(gvy)))

# write to the output file
stack = [px, py, vx, vy, mx, my, gpx, gpy, gvx, gvy]
stack = np.array(stack)
stack = stack.T
np.savetxt('output.csv', stack, '%.6f')
  • 最后我们来看一下我们的EKF在追踪目标的时候的均方误差：
0.0736336090893 0.0804598933194 0.229165985264 0.309993887661
  • 我们把我们的EKF的估计结果可视化：

请输入图片描述

  • 我们放大一个局部看一下：

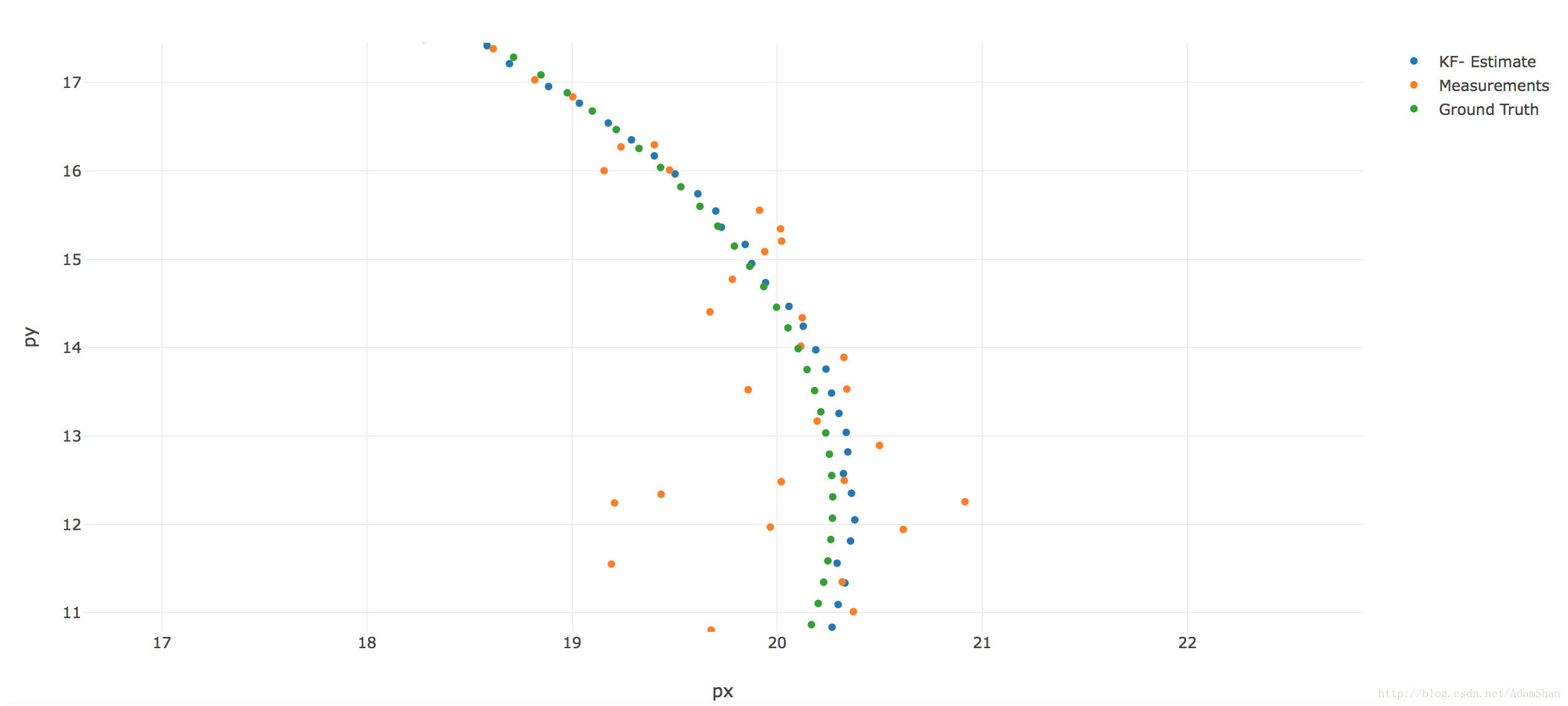
请输入图片描述

  • 其中，蓝色的点为我们的EKF对目标位置的估计，橙色的点为来自LIDAR和RADAR的测量值，绿色的点是目标的真实位置

  • 由此可知，我们的测量是不准确的，因此我们使用EKF在结合运动模型的先验知识以及融合两个传感器的测量的基础上做出了非常接近目标正是状态的估计。

  • EKF的魅力其实还不止在此！我们使用EKF，不仅能够对目标的状态（我们关心的）进行准确的估计，从这个例子我们会发现，EKF还能估计我们的传感器无法测量的量（比如本例中的v,ψ,ψ˙）

  • 那么，扩展卡尔曼滤波就到此结束了，大家可能会问，怎么没看到可视化结果那一部分的代码？哈哈，为了吸引一波人气，请大家关注我的博客，我会在下一期更新中（无损卡尔曼滤波）提供这一部分代码。

  • 最后，细心的同学可能会发现，我们这个EKF执行的效率太低了，实际上，EKF的一个最大的问题就是求解雅可比矩阵计算量比较大，而且相关的偏导数推导也是非常无聊的工作，因此引出了我们下一篇要讲的内容，无损卡尔曼滤波（Unscented Kalman Filter，UKF）

  • 附数据下载链接：http://download.csdn.net/download/adamshan/10033533

参考：

  • https://blog.csdn.net/AdamShan/article/details/78265754

纠错,疑问,交流: 请进入讨论区或 点击加入Q群

获取最新文章: 扫一扫右上角的二维码加入“创客智造”公众号


标签: 无人驾驶汽车系统入门