PythonRobotics机器人算法库-三次样条规划

说明：

• 介绍三次样条规划

• 参考代码

步骤：

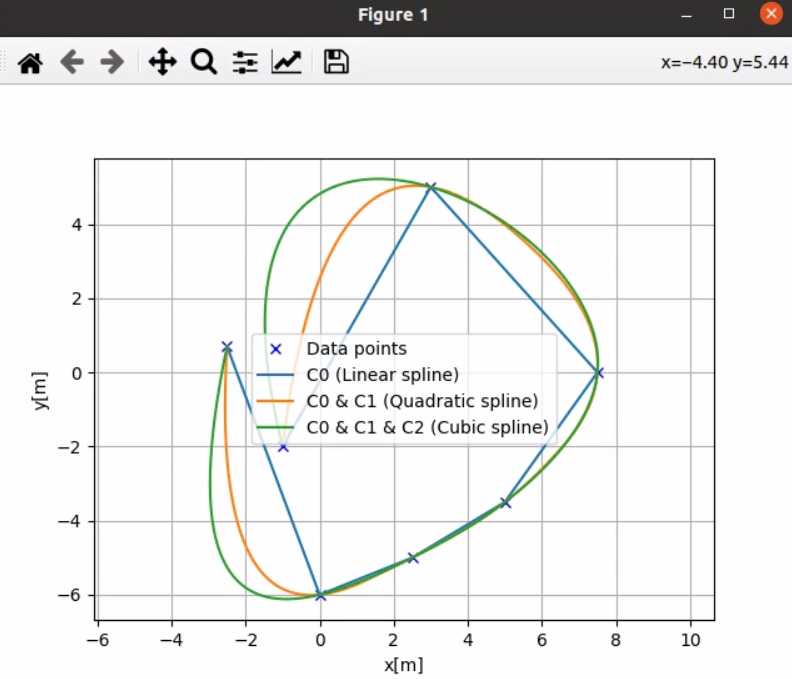
样条曲线连续性

• 样条曲线的平滑度取决于使用哪种样条模型。

• 样条曲线的平滑度表示为C0 C1， 等等。

• 该表示表示曲线的连续性。例如，对于二维空间中的样条曲线：

• C0位置是否连续

• C1切向量是连续的

• C2曲率向量是连续的

• 如下图所示：

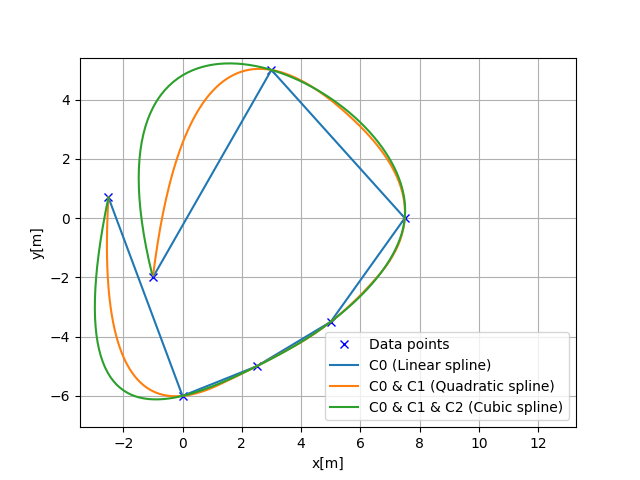
• 三次样条可以生成一条曲线，C0，C1，C2

一维三次样条

• 三次样条插值是在给定多个数据点的情况下，在多个数据点之间进行平滑插值的方法，如下图所示。

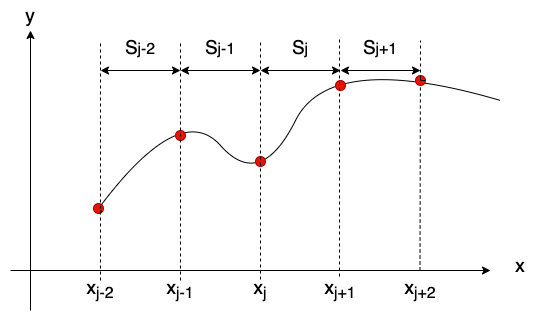
• 它在数据点之间的每个间隔之间进行分隔。

• 每个区间部分由每个三次多项式近似。

• 三次样条使用三次多项式方程进行插值：

约束一：终端约束

约束2：点连续约束

约束3：切向量连续约束

约束4：曲率连续约束

约束 5：终端曲率约束

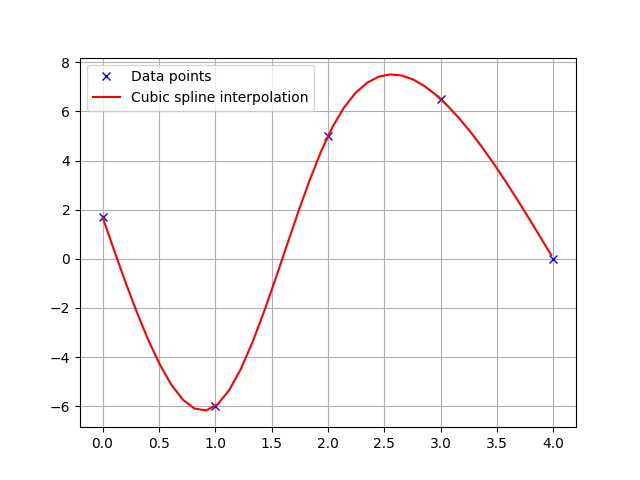
• 例子，插入一维数据点

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(5)
y = [1.7, -6, 5, 6.5, 0.0]
sp = CubicSpline1D(x, y)
xi = np.linspace(0.0, 5.0)
yi = [sp.calc_position(x) for x in xi]
plt.plot(x, y, "xb", label="Data points")
plt.plot(xi, yi , "r", label="Cubic spline interpolation")
plt.grid(True)
plt.legend()
plt.show()

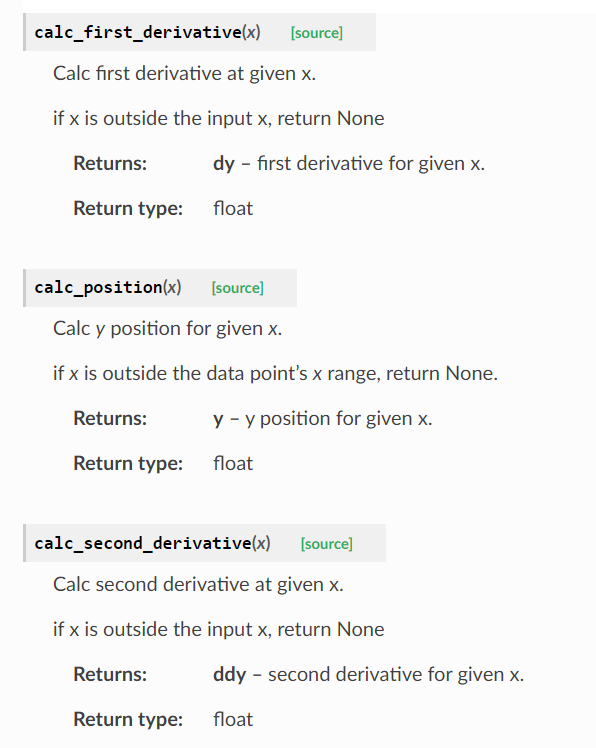
• 二维三次样条

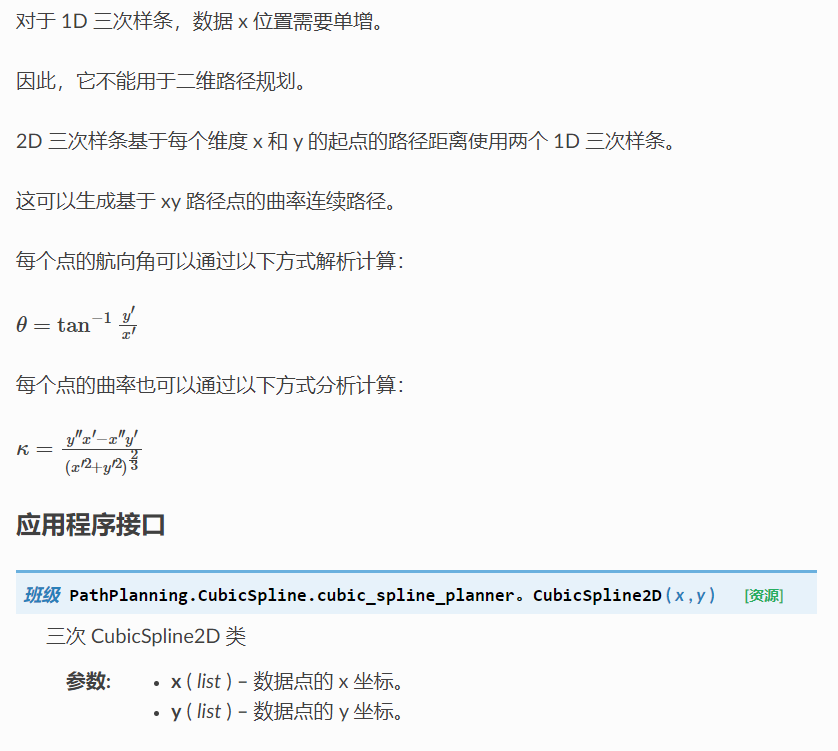
• 例如，可以对二维数据点进行插值

import matplotlib.pyplot as plt
x = [-2.5, 0.0, 2.5, 5.0, 7.5, 3.0, -1.0]
y = [0.7, -6, 5, 6.5, 0.0, 5.0, -2.0]
ds = 0.1  # [m] distance of each interpolated points
sp = CubicSpline2D(x, y)
s = np.arange(0, sp.s[-1], ds)
rx, ry, ryaw, rk = [], [], [], []
for i_s in s:
    ix, iy = sp.calc_position(i_s)
    rx.append(ix)
    ry.append(iy)
    ryaw.append(sp.calc_yaw(i_s))
    rk.append(sp.calc_curvature(i_s))
plt.subplots(1)
plt.plot(x, y, "xb", label="Data points")
plt.plot(rx, ry, "-r", label="Cubic spline path")
plt.grid(True)
plt.axis("equal")
plt.xlabel("x[m]")
plt.ylabel("y[m]")
plt.legend()
plt.show()

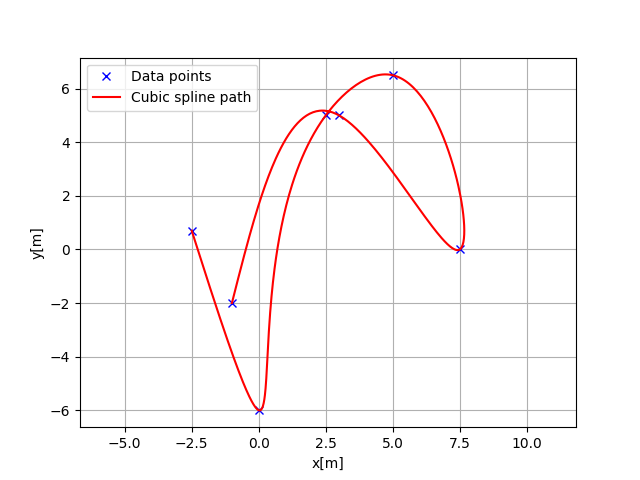
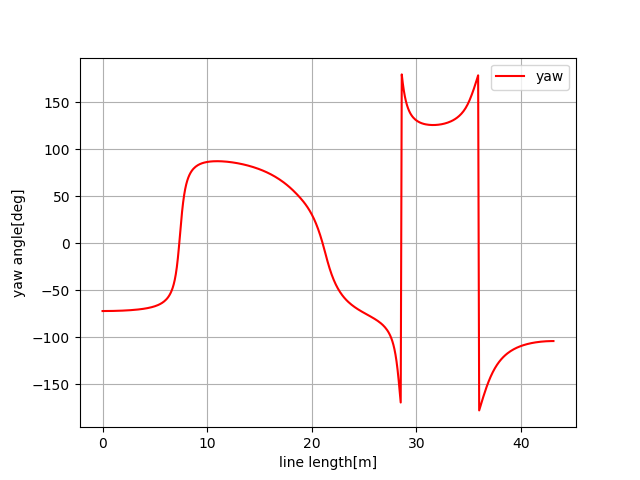
plt.subplots(1)
plt.plot(s, [np.rad2deg(iyaw) for iyaw in ryaw], "-r", label="yaw")
plt.grid(True)
plt.legend()
plt.xlabel("line length[m]")
plt.ylabel("yaw angle[deg]")

plt.subplots(1)
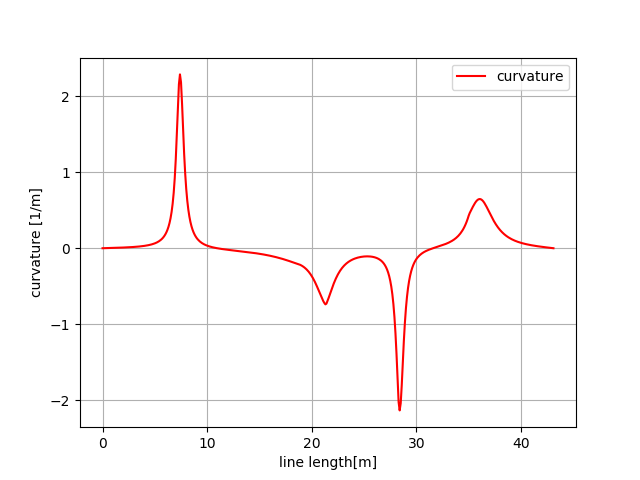
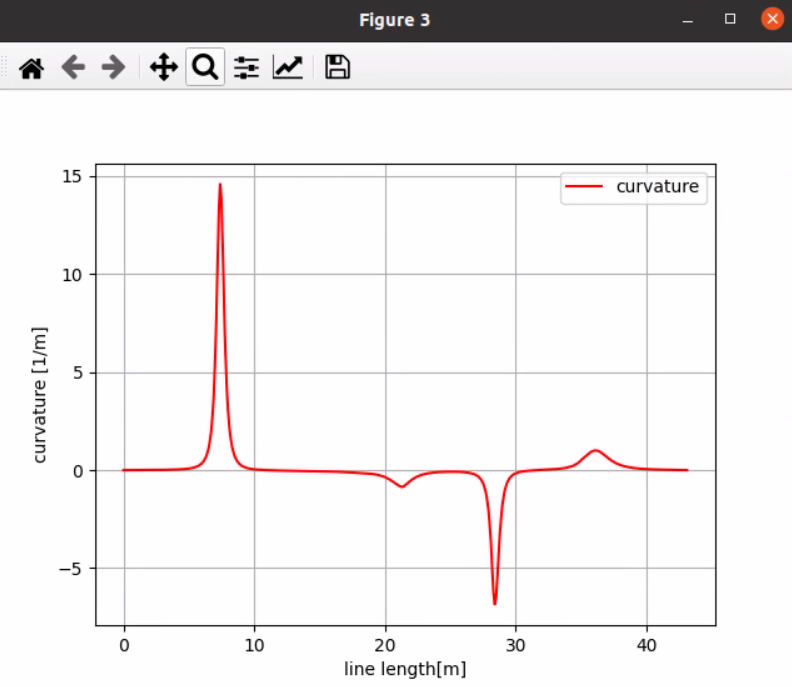
plt.plot(s, rk, "-r", label="curvature")
plt.grid(True)
plt.legend()
plt.xlabel("line length[m]")
plt.ylabel("curvature [1/m]")

• 进入目录PythonRobotics/PathPlanning/CubicSpline

• 执行文件

python3 cubic_spline_planner.py

python3 spline_continuity.py

• 结果如下